【RL学习笔记】Q学习算法

算法

Q 学习算法（Q-Learning Algorithm）的思路比较简单：使用 Q 函数记录每一个状态下每一个动作（action）的期望最大总回报（reward），即 Q 值。在推理时贪心地选择当前状态 Q 值最大的动作，从而达到最大化期望总回报的目的。当问题的状态与动作均为离散时，Q 函数可以使用表格记录，这个表格也称为 Q 表格（Q-Table）。

设：

问题的状态空间为 $S = {1,2,\ldots, m}$；
问题的动作空间为 $A = {1,2,\ldots, n}$；
探索阈值为 $\epsilon\in [0,1]$ （推理时 $\epsilon = 0$ ）；
学习率 $\eta\in [0,1]$ ；
回报衰减率 $\gamma\in [0,1]$ 。

则 Q 学习算法的流程如下：

初始化 Q 表格为零矩阵 $Q=O_{m\times n}$ ；
设初始时间 $t = 0$ ，状态为 $s_t = s_0$ ；
选择动作 $a_t$ ：取随机数 $r\in[0,1]$ ，若 $r<\epsilon$ ，则当前为探索阶段，从 $A$ 随机选取一个动作；否则 $a_t = \argmax_{j\in A} Q_{s_t, j}$ ；
与环境交互，执行动作 $a_t$ ，并获得状态 $s_{t+1}$ 、回报 $r_t$ ；
按照 Bellman 方程更新Q表格： $Q_{s_t, a_t} \leftarrow (1-\eta) Q_{s_t, a_t} + \eta(\gamma\max_{j\in A} Q_{s_{t+1},j} + r_t),$ 其中 $\max Q_{s_{t+1},j}$ 为转移后的状态 $s_{t+1}$ 下最大的Q值，加上 $r_t$ ，组成转移前状态 $s_t$ 下 $a_t$ 操作的Q值。将其与原来的 $Q_{s_t, a_t}$ 加权平均就得到了更新后的Q值。
时间 $t\leftarrow t+1$ ，回到第 3 步。

实现

Frozen Lake

以 Gym 的 Frozen Lake 环境为例，其状态空间与动作空间都是离散的，因此适合使用 Q 表格。这个环境共有 $4^2=16$ 种状态，4 种动作，分别对应上下左右四个移动方向。环境中slippery引入的不确定性太大（每次行动只有 $1/3$ 的概率能真正前往指定的方向），因此这里创建环境时is_slippery一项设为False。

实现如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
import gymnasium as gym
import numpy as np
from random import random

env = gym.make('FrozenLake-v1', map_name="4x4", is_slippery = False)

n_actions, n_states = env.action_space.n, env.observation_space.n
lr, gamma = 0.2, 0.6
total = 1000

Q_table = np.zeros((n_states, n_actions))
state, info = env.reset()
for t in range(total):
    # 选择动作
    epsilon = 1 - t / total
    if random() < epsilon: # 探索
        action = env.action_space.sample()
    else:
        action = Q_table[state].argmax(0)

    org_state = state
    state, reward, terminated, truncated, info = env.step(action)
    if state == n_states-1: # 抵达终点，获得奖励
        reward = 20
    elif terminated:        # 掉进洞里，给予惩罚
        reward = -5
    else:                   # 让agent尽快抵达终点
        reward = -1

    # 更新Q值
    Q_table[org_state, action] = ((1 - lr) * Q_table[org_state, action]
                                  + lr * (reward + gamma * Q_table[state].max()))

    if terminated or truncated:
        state, info = env.reset()

原环境提供的回报函数所含的信息较少（仅在抵达终点时为 1，其余情况均为 0），不利于算法的收敛，因此我在实现中重新设计了回报函数。此外，训练时采用线性衰减的探索阈值 $\epsilon$ ，即训练初期倾向于探索（exploration），后期倾向于开发（exploitation）。

训练时每轮的 t 与该轮获得的总 reward 的折线图如下：

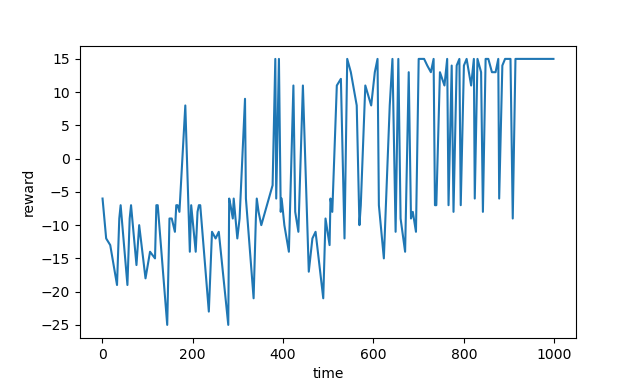
推理时算法选择的路线如下图，确实是最优路线之一。

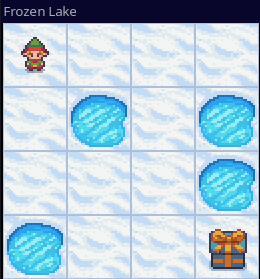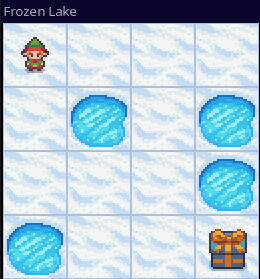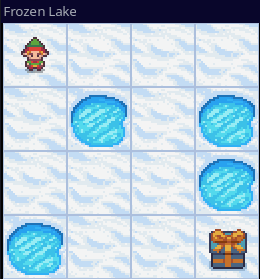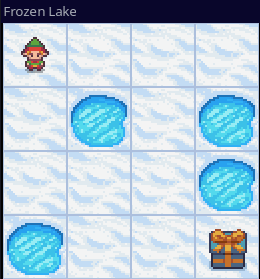
除了 Frozen Lake，这个方法也可以用来求解 Gym 提供的 Cliff Walking、Taxi 与 Blackjack。但是，随着问题规模的增大，训练步数也需要相应地增加。

Cliff Walking

这个环境有 48 种状态和 4 种动作，因此 Q 表格内共有192项。以下是训练了 10,000 步的结果（平均每项 52 步）：

Taxi

这个环境有 500 种状态和 6 种动作，对应 Q 表格的 3000 项。以下是训练了 200,000 步的结果（平均每项 67 步）：

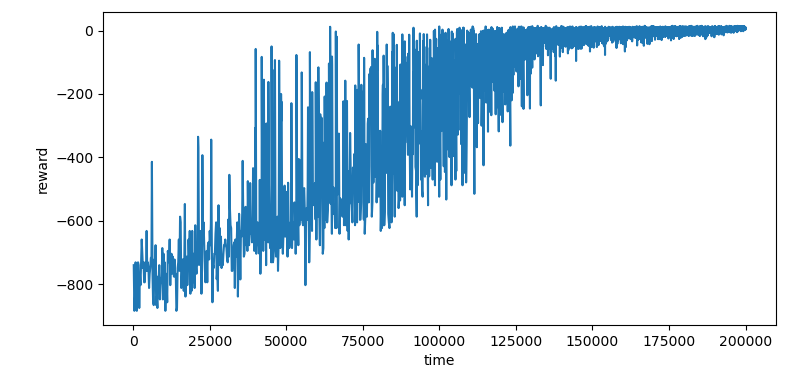
Blackjack

Blackjack 有 $32\times 11\times 2=704$ 种状态和 $2$ 种动作，在处理时需要将离散的状态向量映射到非负整数域内。这个游戏的状态转移存在不确定性，即使是充分训练（ $5\times 10^6$ 步）的Q表格也只能将胜率从完全随机时的 28.2% 提升到 39.3%。

分析

优点

算法简单，易于理解和实现。

局限性

基于 Q 表格的 Q 学习算法只能处理输入输出都是离散的问题；
基于 Q 表格的 Q 学习算法不能跨实例学习，即在遇到新的问题实例时，需要从 0 开始重新探索；
基于 Q 表格的 Q 学习算法难以处理训练过程中没有见过的状态；
当状态空间或动作空间很大时，Q 表格的规模也会很大，从而需要更长的学习时间。

上述问题可以通过引入神经网络缓解，即深度 Q 学习算法（Deep Q-Learning Algorithm）。