【RL学习笔记】深度Q学习算法与经验回放

深度Q学习算法

理论

深度Q学习算法（Deep Q-Learning Algorithm）是将 Q 表格替换为神经网络的 Q 学习算法，由 DeepMind 的 Mnih et al. ^[1]^[2]提出。 Q表格本质上是一个函数 $f: S\times A \rightarrow \mathbb{R}$，我们自然也可以使用神经网络构造这个函数，让它可以处理连续的状态和动作。此外，使用神经网络还有一个好处：我们可以向神经网络输入实例信息 $m\in M$ ，使之可以跨实例学习函数 $f: M\times S\times A\rightarrow \mathbb{R}$ 。也就是说，Agent可以将其在实例 $m_1,~~m_2,~~\ldots~m_n$上学习到的经验迁移到未曾见过的实例 $m_{n+1}$ 上，增强模型的泛化性能，减少其探索新实例所需的时间。

网络更新方程的设计（以 Bellman 方程为基础）： $$Q(s_t, a_t) \leftarrow (1-\eta) Q(s_t, a_t) + \eta(\gamma\max_{j\in A} Q(s_{t+1}, j) + r_t)$$

求更新前与更新后的差分： $$\Delta Q(s_t, a_t) = -\eta Q(s_t, a_t) + \eta(\gamma\max_{j\in A} Q(s_{t+1},j) + r_t)$$

即： $$\Delta Q(s_t, a_t) = \eta(\gamma\max_{j\in A} Q(s_{t+1},j) + r_t - Q(s_t, a_t))$$

在理想情况下充分训练时，应当有 $$\lim_{t\rightarrow \infty}\Delta Q(s_t, a_t) = 0$$

也就是说，训练的目标应当是最小化 $\Delta Q(s_t, a_t)$，即目标函数为： $$L(\theta) = \mathrm{MSE}(Q(s_t, a_t),~\gamma\max_{j\in A} Q(s_{t+1},j) + r_t)$$ 其中的 $\mathrm{MSE}$ 也可以替换为其它的损失函数。

实现

下面以CartPole-v1环境为例编写训练程序。

引入相关的库以及定义一些超参数：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
from random import random, randint
import gymnasium as gym
import torch
import torch.nn as nn
from tqdm import tqdm

n_actions = 2
n_states = 4
lr = 3e-4
discount = 0.95
batch_size = 128
epochs = 5000

定义神经网络，这里定义了一个简单的三层神经网络，其中输出层没有添加激活函数是因为激活函数会限制网络的值域至 $R_{act}$ ，设Q函数的值域是 $R_Q$，$R_Q\nsubseteq R_{act}$ 时损失函数难以收敛，影响训练效果：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
class Net(nn.Sequential):
    norm_vector = torch.tensor([0.5, 1.0, 0.21, 0.5])

    def __init__(self, in_feats = n_states, out_feats = n_actions, hidden = 32):
        super().__init__(
            nn.Linear(in_feats, hidden),
            nn.SiLU(),
            nn.Linear(hidden, hidden),
            nn.SiLU(),
            nn.Linear(hidden, out_feats),
        )

    def forward(self, state):
        x = state/self.norm_vector # 归一化
        y = super().forward(x)
        return y

定义网络、优化器与损失函数：

1
2
3
net = Net()
optimizer = torch.optim.AdamW(net.parameters(), lr=lr, amsgrad=True)
criterion = nn.SmoothL1Loss() # 发现L1的效果比L2要好

训练过程（原环境提供的 reward 恒为 1，信息太少，因此这里改用自定义的 reward，在倾角过大或位置过远时进行惩罚）：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
env = gym.make("CartPole-v1")
state, info = env.reset()
for t in tqdm(range(epochs)):
    # 前向传播
    loss = 0.0
    epsilon = 1 - t / epochs  # 动态调整epsilon
    for _ in range(batch_size):
        # 选择action =========================
        row = net(state)
        if random() < epsilon: # exploration
            action = randint(0, n_actions-1)
        else:
            action = row.squeeze().argmax().item()

        # 执行action =========================
        state, reward, terminated, truncated, info = env.step(action)
        # 使用自定义的reward
        reward = -20.0 if terminated else 0
        if abs(state[2]) > 0.1: # 限制倾角
            reward += -1.0
        if abs(state[0]) > 0.3: # 限制位置
            reward += -2.0
        if reward >= 0:
            reward = 1.0

        # 计算loss =========================
        with torch.no_grad():
            if terminated:
                curr_q = torch.tensor(reward)
            else:
                curr_q = net(state).max() * discount + reward
        loss += criterion(row[action], curr_q)

        if terminated or truncated:
            state, info = env.reset()

    # 反向传播
    optimizer.zero_grad()
    (loss/batch_size).backward()
    torch.nn.utils.clip_grad_value_(net.parameters(), 1)
    optimizer.step()
env.close()
# 保存checkpoint
torch.save(net.state_dict(), "cartpole.ckpt")

推理：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
env = gym.make("CartPole-v1", render_mode="human")
state, info = env.reset()
with torch.no_grad():
    for t in range(2000):
        row = net(state)
        action = row.squeeze().argmax(0).item()
        print(row)
        state, reward, terminated, truncated, info = env.step(action)
        if terminated or truncated:
            state, info = env.reset()
env.close()

不出意外的话，运行程序后可以看到类似于这样的动画，说明这个算法以及我们编写的程序都是有效的：

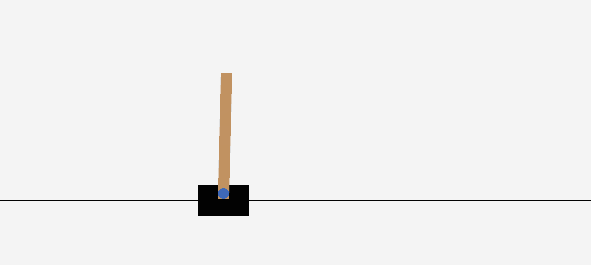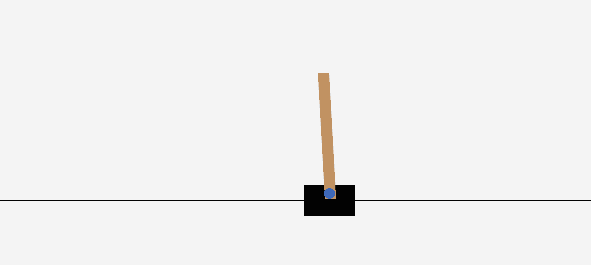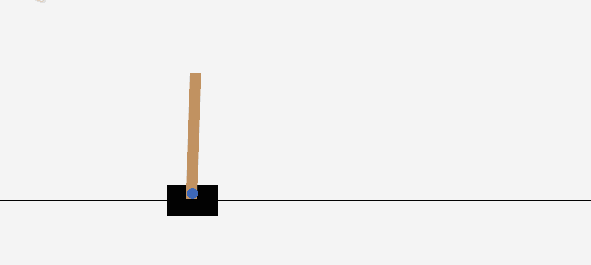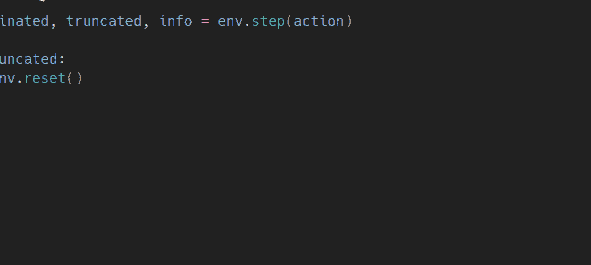
完整的程序见Github Gist，模型权重可以从这里下载（虽然自己训练一个也不费事）。

经验回放

理论

上面的训练 Q 网络的方式存在一些问题，例如

样本的利用率低：每次采样只对应一次前向传播，采样得到的样本未被充分利用；
样本的时序关联性大：每次采样在时间上是高度相关的，上一次采样的末状态就是下一次采样的初始状态，影响训练效果；
训练速度慢：每次前向传播只传播一组数据，速度较慢。

为了缓解上述问题，Mnih et al.^[2] 在提出深度 Q 学习的同时也提出了经验回放（Experience Replay）策略。其主要思想是将采样与训练分离，采样时在记忆中保存采样的记录，训练时随机从记忆中选取样本进行前向与反向传播，从而降低样本间的时序关联性与提高样本利用率。

注意到在算法中，每一步训练需要四个值：当前状态 $s_t$、动作 $a_t$、回报 $r_t$ 以及采取动作后的状态 $s_{t+1}$，因此每一次采样后只需要在记忆中保存这四个值，称为 experience 四元组 $e_t=(s_t,~a_t,~r_t,~s_{t+1})$。

实现

库、超参数、网络结构以及推理部分均沿用上面的代码以便比较，只替换训练部分，然后新增 Experience 类与 Memory 类用于存储和管理样本。以下是 Experience 类与 Memory 类的代码，这里使用队列存储最新的 batch_size*10 条记录：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
from typing import NamedTuple, Union

class Experience(NamedTuple):
    '''experience四元组'''
    state: np.ndarray
    action: int
    reward: float
    next_state: np.ndarray

class Memory(object):
    '''存储固定数量记录的队列'''
    def __init__(self, buffer_size: int):
        self.buffer_size = buffer_size
        self.buffer: list[Union[Experience, None]]
            = [None for _ in range(self.buffer_size)]
        self.count = 0

    def append(self, exp: Experience):
        '''增加记录，如果buffer已满则替换最早的记录'''
        self.buffer[self.count%self.buffer_size] = exp
        self.count += 1

    def sample(self, k: int):
        '''随机选取k个experience，打包好返回'''
        if self.count < self.buffer_size:
            pool = self.buffer[:self.count]
        else:
            pool = self.buffer
        exp: list[Experience] = random.choices(pool, k=k) # type: ignore
        # 打包成 Tensor
        states = torch.from_numpy(np.array([e.state for e in exp]))
        actions = torch.tensor([e.action for e in exp])
        rewards = torch.tensor([e.reward for e in exp])
        next_states = torch.from_numpy(np.array([e.next_state for e in exp]))
        return states, actions, rewards, next_states

memory = Memory(batch_size*10)

采样的部分与原来相同，而在训练的部分，因为这里训练时前向和反向传播都只有一步，所以在计算target_q时不需要像原文所述冻结权重，只要在其后增加.detach()确保反向传播时target_q的梯度不被传播就行。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
env = gym.make("CartPole-v1")
state, info = env.reset()
batch_index = torch.arange(batch_size)
for t in tqdm(range(epochs)):
    # 采样 =========================================
    epsilon = 1 - t / epochs  # 动态调整epsilon
    for _ in range(batch_size//4 if t >= 1 else batch_size):
        if random.random() < epsilon: # exploration
            action = random.randint(0, n_actions-1)
        else:
            action = net(state).squeeze().argmax().item()

        org_state = state
        state, reward, terminated, truncated, info = env.step(action)
        # 使用自定义的reward
        reward = -20.0 if terminated else 0
        if abs(state[2]) > 0.1: # 限制倾角
            reward += -1.0
        if abs(state[0]) > 0.3: # 限制位置
            reward += -2.0
        if reward >= 0:
            reward = 1.0
        # 加入记忆
        memory.append(Experience(org_state, action, reward, state))

        if terminated or truncated:
            state, info = env.reset()

    # 训练 =========================================
    states, actions, rewards, next_states = memory.sample(batch_size)
    # 前向传播
    pred_q = net(states)[batch_index, actions]
    target_q = (net(next_states).max(dim=-1).values * discount + rewards).detach()
    loss = criterion(pred_q, target_q)
    # 反向传播
    optimizer.zero_grad()
    loss.backward()
    torch.nn.utils.clip_grad_value_(net.parameters(), 1)
    optimizer.step()

env.close()
# 保存checkpoint
torch.save(net.state_dict(), "cartpole-replay.ckpt")

完整程序见 Github Gist，运行程序，发现两个程序在batch_size=128和epochs=5000的情况下，原来的程序在我的轻薄本上需要训练 3 分钟，而得益于批处理的训练过程以及采样数的减少，有经验回放的训练只要 15 秒就能达到更好的效果。

继续增加batch_size或epochs，效果更佳。以下是batch_size=256、epochs=5000的结果，训练只花了 28 秒。

参考文献

[1] Mnih, V., Kavukcuoglu, K., Silver, D., Graves, A., Antonoglou, I., Wierstra, D., & Riedmiller, M. (2013). Playing Atari with Deep Reinforcement Learning (arXiv:1312.5602). arXiv. https://doi.org/10.48550/arXiv.1312.5602 ⤶

[2] Mnih, V., Kavukcuoglu, K., Silver, D., Rusu, A. A., Veness, J., Bellemare, M. G., Graves, A., Riedmiller, M., Fidjeland, A. K., Ostrovski, G., Petersen, S., Beattie, C., Sadik, A., Antonoglou, I., King, H., Kumaran, D., Wierstra, D., Legg, S., & Hassabis, D. (2015). Human-level control through deep reinforcement learning. Nature, 518(7540), Article 7540. https://doi.org/10.1038/nature14236 ⤶⤶